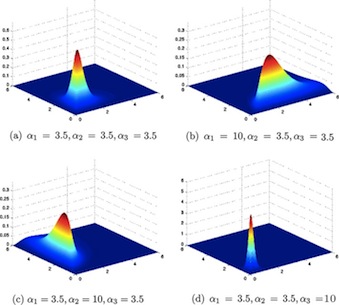
The Normal Distribution
\[ \sim Nl(\mu, \sigma^2) \]
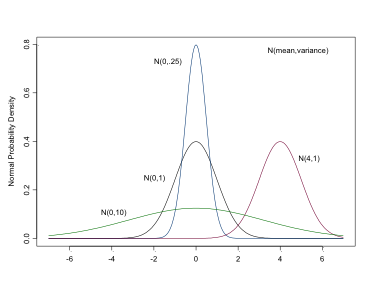
The Normal Distribution
- continuous variables or parameters
- dnorm(mean, precision)
- NB precisions, \(1/\sigma^2\)
- flat prior, very large variance, very small precision
- dnorm(0,.0001) , dnorm(0,1.0E-4).
- half-normal to restrict
- dnorm(0,1.0E-4)I(0,)